Leetcode 454. 4Sum II

https://leetcode.jp/leetcode-454-4sum-ii-%E8%A7%A3%E9%A2%98%E6%80%9D%E8%B7%AF%E5%88%86%E6%9E%90/
摘要:
个人认为本题与Two Sum属于同类型题目，主要考察HashMap，而3Sum与4Sum又是另外一个类型，均可使用双指针思路来解题。

分析本题之前，我觉得有必要说下本题与前一集4Sum的区别，虽然都是求4个数和为某个Target的题目，但是区别在于，本题是在4个数组中分别找4个数字，前一题则是在一个数组中找。我们要明白他们在本质上的不同，才能理解为什么不能使用同一种解题方法。当在一个数组中找4个数字时，我们解法使用的时间复杂度为O(n^3)，前两层循环是在找前两个数，第三层循环使用双指针来找后两个数。其实本题也能使用该方法，但是难点在于无法剪枝！4Sum虽然使用了O(n^3)的时间复杂度，但是剪枝操作让其执行次数远远小于n的三次方，剪枝的核心在于，因为只有一个数组，当它排序之后，如果当前数已经大于Target，那么在它后面的其他数字肯定也都大于Target，此时可以结束循环。而回到本题，我们需要在4个数组中分别挑一个数出来，这样，即使当前数字大于Target，我们也不能确定其他数组中挑出的数字是否也都大于Target，这样一来，就没有办法进行剪枝操作了。

那么本题该如何解呢？上文已经说过，本题其实与Two Sum很相似，我们将4个数组分成2组，A，B和C，D，先使用两层循环遍历A和B中所有元素两两之和，并将结果保存至HashMap，其中key为两元素之和，value为该和出现的次数。之后再使用两层循环遍历C和D中所有元素两两之和，并查看该和的相反数在map中存在的个数，并将个数累加至返回结果即可。

lc142 Linked List Cycle II

快指针任何时候走的距离一定为慢指针的 2 倍

fast 指针在任何时候走的距离一定是 slow 指针的 2 倍，这个结论我想大家都没什么疑问，知道了这个结论之后，我们再来看一下下面这幅图：

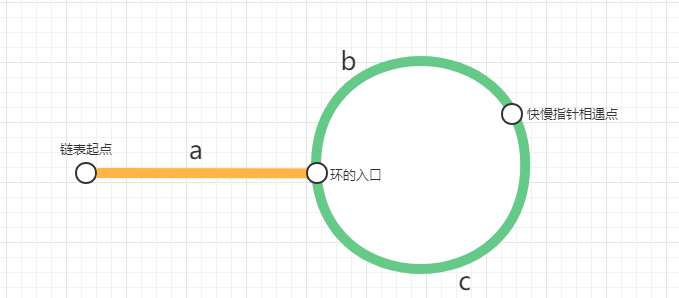
上图中以节点为划分，有三段链表，a，b，c 分别表示三段的距离，我们假设当快慢指针相遇的时候，快指针已经在环中走了 n 圈，那么就可以得到快指针走过的距离为：a+n*(b+c)+b，而慢指针走过的距离为 a+b，根据快指针走的路程一定是慢指针的两倍，可以得到如下等式：

a+n(b+c)+b = 2(a+b)，最终经过转换，得到 a=(n-1)*(b+c) + c。

到这里可能有人会有疑问，快慢指针相遇的时候，为什么慢指针一定没有走完一圈呢？如果慢指针也走了 m 圈，那么慢指针走过的距离就是 a+m*(b+c)+b 了，但是这其实是不可能的。

为什么快慢指针相遇时慢指针没有走完一圈

我们假设这个环的长度为 x，那么当 slow 指针走完一圈时，需要走 x 步，而当 slow 指针走完 x 步，fast 指针已经走了 2x 步了，也就是走了两圈了，那么他们一定在某一个点相遇过了（因为他们不可能错过相遇点），所以当快慢指针第一次相遇时，慢指针是不可能走完一圈的。

利用第三个指针找到环的位置

继续回到上面的等式：a=(n-1)*(b+c) + c，然后我们可以发现，其实 b+c 正好等于环的长度，也就是说：从链表头部到入环的距离（a）恰好等于从相遇点到入环点的距离（c）再加上 n-1 圈个环的长度。

这时候就有个有趣的现象了，如果 slow 和 fast 相遇了，那么这时候我们再定义一个指针指向链表起点，一次走一步，slow 指针也同步继续往后走，那么这两个指针就一定会在链表的入口位置相遇。